-
프로그래머스 Lv2 땅따먹기Computer Science/프로그래머스 2023. 10. 6. 11:22
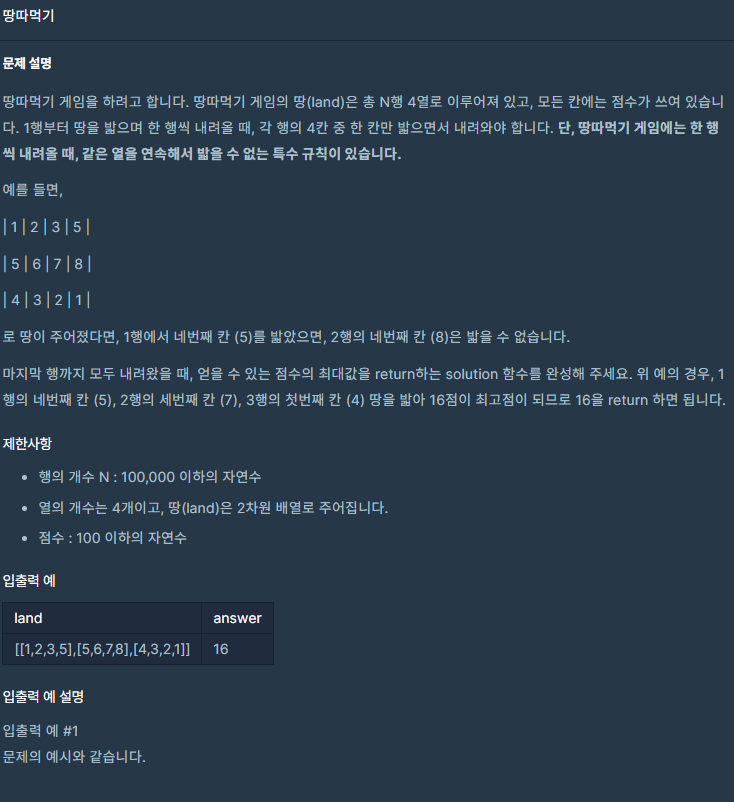 더보기
더보기이 문제는 DP로 풀면 된다.
0번째 행에서 접근하는 방법을 찾아보자.
1 2 3 5 5 6 7 8 4 3 2 1 100 1 2 3 1번째 행 입장으로 생각하면
1번째 행에서 0번 열을 선택하면 {2, 3, 5}중 한가지를 선택해야 하므로 5를 선택한다.
1번째 행에서 1번 열을 선택하면 {1, 3, 5}중 한가지를 선택해야 하므로 5를 선택한다.
1번째 행에서 2번 열을 선택하면 {1, 2, 5}중 한가지를 선택해야 하므로 5를 선택한다.
1번째 행에서 3번 열을 선택하면 {1, 2, 3}중 한가지를 선택해야 하므로 3을 선택한다.
선택한 값을 다음 행에 누적시킨다.
1 2 3 5 10 11 12 11 4 3 2 1 100 1 2 3 2번째 행 입장으로 생각하면
2번째 행에서 0번 열을 선택하면 {11, 12, 11}중 한가지를 선택해야 하므로 12를 선택한다.
2번째 행에서 1번 열을 선택하면 {10, 11, 12}중 한가지를 선택해야 하므로 12를 선택한다.
2번째 행에서 2번 열을 선택하면 {10, 11, 11}중 한가지를 선택해야 하므로 11를 선택한다.
2번째 행에서 3번 열을 선택하면 {10, 11, 12}중 한가지를 선택해야 하므로 12를 선택한다.
규칙을 찾으면 다음 행에 무엇을 선택했는지에 따라서 이전 행에서 선택 할 수 있는 열이 정해지고
그 열 중 최대값을 찾으면 되는 문제이다.
for(int i = 0; i < land.size() - 1; ++i) { land[i + 1][0] += max(land[i][1], max(land[i][2], land[i][3])); land[i + 1][1] += max(land[i][0], max(land[i][2], land[i][3])); land[i + 1][2] += max(land[i][0], max(land[i][1], land[i][3])); land[i + 1][3] += max(land[i][0], max(land[i][1], land[i][2])); }더보기선택 가능한 열이 4개이므로 4가지의 경우의 수를 생각해야하고 마지막 행에서 최대 값을 찾으면 된다.
#include <iostream> #include <vector> using namespace std; int solution(vector<vector<int> > land) { int answer = 0; for(int i = 0; i < land.size() - 1; ++i) { land[i + 1][0] += max(land[i][1], max(land[i][2], land[i][3])); land[i + 1][1] += max(land[i][0], max(land[i][2], land[i][3])); land[i + 1][2] += max(land[i][0], max(land[i][1], land[i][3])); land[i + 1][3] += max(land[i][0], max(land[i][1], land[i][2])); } int n = land.size() - 1; answer = max(land[n][0], max(land[n][1], max(land[n][2], land[n][3]))); return answer; }'Computer Science > 프로그래머스' 카테고리의 다른 글
프로그래머스 Lv2 올바른 괄호 (1) 2023.10.06 프로그래머스 Lv2 다음 큰 숫 (0) 2023.10.06 프로그래머스 Lv2 멀리 뛰기 (0) 2023.10.06 프로그래머스 Lv2 숫자 블록(소수) (0) 2023.10.05 프로그래머스 Lv2 숫자의 표현 (1) 2023.10.05